What’s the shortest word that contains ‘ABCDE’ and so on…

Contiguous letter sequences

Haggard Hawks—one of my favorite Twitter accounts, and the subject of a different project once before—tweeted out this fun fact.

GOLDFINCHES contains the letters CDEFGHI.
JASMINELIKE contains the letters IJKLMN.
PROPINQUITIES contains the letters OPQRST.

Which got the ol’ thinker thinkin’.

The code for this is relatively straightforward, so I wont belabor it, but I will admit I had to think a bit about what exactly I wanted to do. I came up with

For each subsequence of the alphabet, what is the shortest word in my dictionary(we'll come back to this) that contains all letters in this subsequence?

A few points:

• I wanted the shortest word as a way to make the solutions more unique, and more “purely” about the letters.
• I wanted to consider all subsequences because I predicted it would make for a better visualization and decomposition of the alphabet than random splittings of letters.

The coding part

The most challenging of the coding component was an organized and reasonably efficient way to run through all words in the dictionary and all subsequences. Since the dictionary is long in comparison to the number of subsequences—(n^2 + n) / 2)-n=325 because I ignore single letters—I knew that I’d want to scroll through the dictionary and check which of the subsequences were there. Thus I made a dict, with keys all the subsequences and values as empty lists, and then checked if the alphabetized-uniqued version of the word contained the subsequence. If so, I added it to the dictionary in length order. This worked and wasn’t too slow, even for 300k words.

If I were really flexing, I’d have made the subsequences into a trie, and traversed that to reduce the number of checks, but it didn’t seem worth it since the run-time was so small already.

Visualization

After running through the above, I knew in my mind that I wanted some matrix presentation of the data, but for the life of me couldn’t make sense of how to do it. I kept thinking that the rows and columns would be letters contained in the sequence, but this actually becomes sort of a tensor(3-dimensional matrix), in that there is a matrix of containment for every pair of letters. After far too long I realized that starting letter and ending letter uniquely identify the subsequence, and realized what I wanted.

I used Tableau to simplify generating the graphics, which for this simple of a project, was plenty.

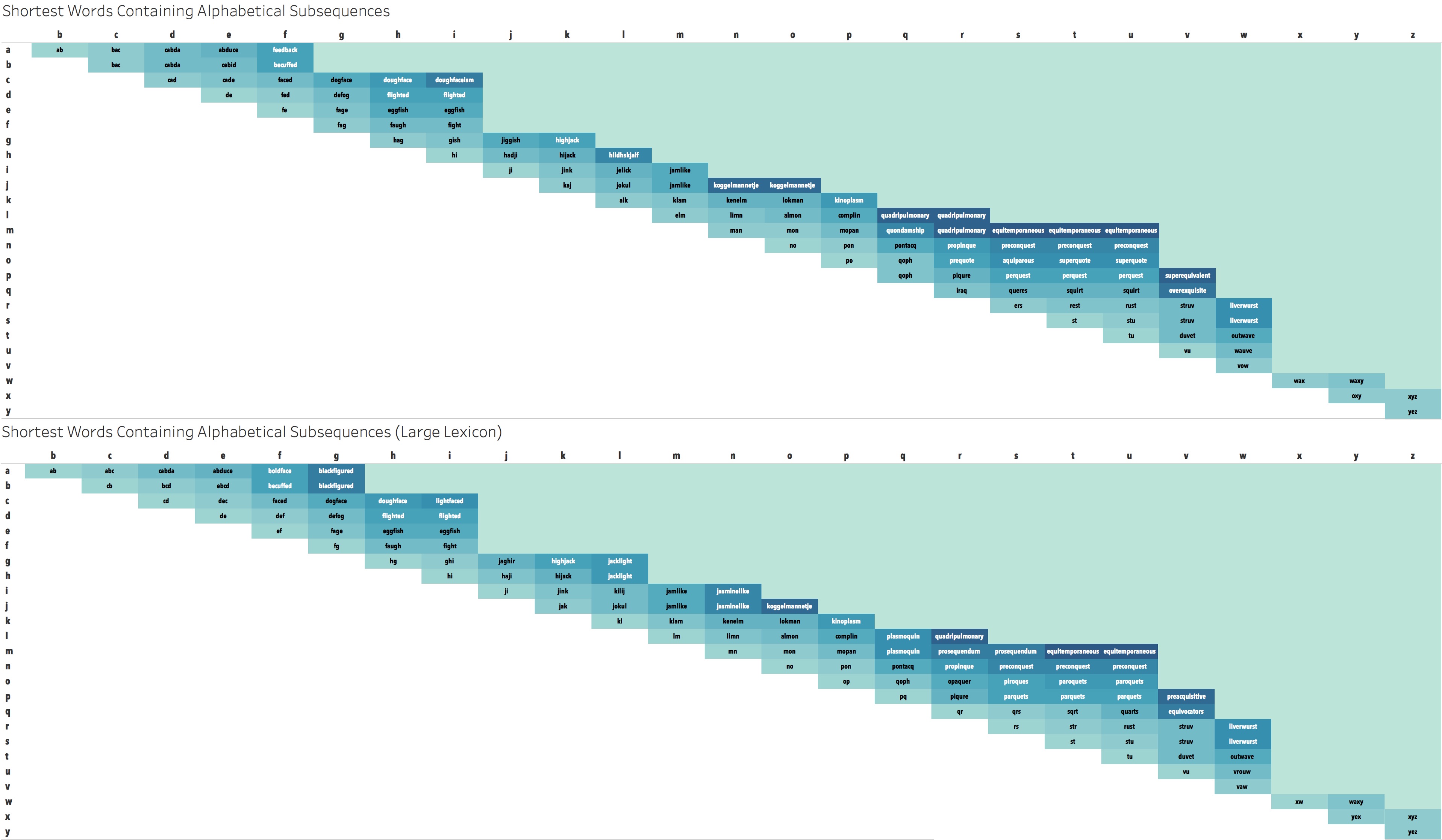
In the above you’ll notice two matrices because I used two separate word lists. Originally, I just used the unix wordlist, but I immediately noticed I didn’t find JASMINELIKE in my analysis, or even another word that contained IJKLMN. This bothered me, so I looked around for a longer wordlist similar to the unix one. I found this one. I liked how similar the wordlists were, and this one is about 50% larger. You’ll notice that the larger dictionary does, in-fact, have jasminelike, and adds some other good words on the outskirts of this matrix.

I liked that the big stair steps in the matrices show where certain letters have a lot less words.

Efficiency

Because I was thinking about how short the words were in terms of their subsequence, I decided to compute efficiency of the words. Hueristically, this meant how many letters beyond the subsequence were necessary to create the word. We expect that as the subsequence grows in length, the efficiency will also decrease, and that was true.

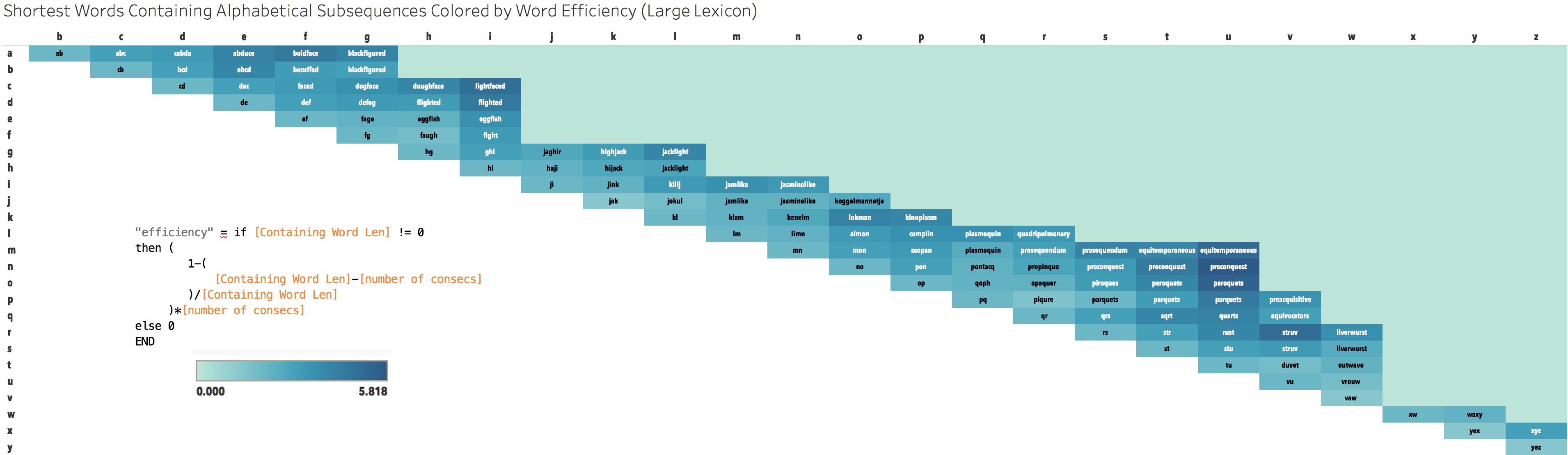
To compute this I used the following formula:

(
  1-([Containing Word Len]-[number of consecs])/[Containing Word Len]
)*[number of consecs]

Which is the percentage of the number of unnecissary letters multiplied by the number of consecutive letters. The reason for skewing by consecutive letters is to accomidate that it’s harder and harder to make a word as the number of letters increase.

Some analysis

If I wanted to recreate the original tweet with the shortest possible words:

LIGHTFACED is a shorter word for CDEFGHI
JASMINELIKE is the shortest for IJKLMN
PAROQUETS is shorter for OPQRSTU

If I wanted the shortest total letters to express the alphabet:

AB,CD,FE,HG,JI,KL,MN,PO,QR,ST,VU,XW,YEZ

Which isn’t very interesting, so I switched to shortest number of words and minimizing letters within that:

BOLDFACE,HIGHJACK,PLASMOQUIN,LIVERWURST,XYZ

Note that this required a bit more coding, to find the optimal sequence.